Fizikailag úgy értem, mint egy objektum lendületét, amely valamilyen helyzetben adott körül forog. A képletre azonban nem tudok fizikai magyarázatot adni. Miért szorozzuk a lineáris momentumot a pozícióval? Miért a szögimpulzus a pozíció függvénye? span class = "math-container"> $ L = mv * r $ (a kar p * r = karja )

(Ez egy késői válasz , de remélem, hogy mégis mélyebb és tisztább betekintést nyújthat a kérdésbe, úgy képzelem, hogy Noether tétele nem oldotta meg a problémáit):

Ez nagyon egyszerű: a másik kérdésben megértette a lineáris momentum fogalmát, most már csak a lever .

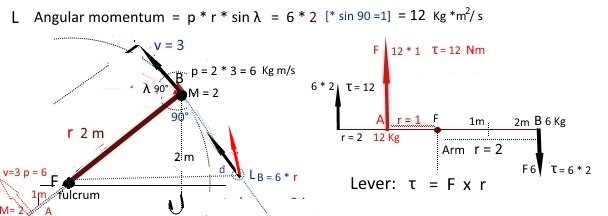
Képzeljük el, hogy a B labda ugyanaz a labda, mint a lineáris-impulzus kérdésben ( $ m $ = $ 2 $ $ Kg $ ) itt utazott: $ v $ = $ 3 m / s $ és $ momentum $ = $ 6 $ $ Kg $ $ m / s. $

Képzelje el, hogy van rajta egy zsinór és egy horog, és hogy ezt a horgot egy csap fogja meg $ F $ . Mi fog történni? A $ B $ elkezdi forogni a támaszpont körül $ F $ (vázlat a bal oldalon). A mozgás iránya merőleges lesz a sugárra (egyenesre), ezért a szög $ 90 ° $ és $ sine lesz. A $ értéke $ + 1 $ lesz.

Ebben az új forgatókönyvben (vázlat a jobb oldalon; ugyanaz, mint egy kar ban) a kifejtett nyomaték a sugártól is függ, a test távolsága a támaszponttól, amely a kar karja. A nyomaték nagysága a $ r $ értékétől függ. $ 6 kg $ súly 12 $ $ $ Nm $ a $ 2 $ $ m $ távolságra, és meglesz csak akkor egyenlegezzen, ha (a másik karra) $ 6 Kg $ súlyt tesz fel 2 m $ $ vagy súlya 12 $ $ $ Kg $ a 1 millió dollárnál .

Ha megértette a kar fogalmát, könnyen megértheti a $ * szögletes $ span képletének fizikai magyarázatát > $ momentum * $ . Ugyanígy, ha B ( $ m $ = $ 2 $ ) az óramutató járásával ellentétes irányban forog a $ v $ = $ 3 m / s $ ( $ linear $ span> $ momentum $ = $ 6 $ ) távolságra $ 2 m $ a támaszponttól szögletű lesz (6 * 2 =) 12 Kg * m ² / s). Ha a B-ről lógó vonal csak $ 1 m $ hosszú lett volna, akkor a $ L $ nagysága been (6 * 1) = 6.

Hasonlóképpen, ha egy másik A törzs ( $ m $ = $ 2 $ , $ v $ = $ 3 $ , $ p $ = $ 6 $ ) az óramutató járásával megegyező irányban forog a másik karon, nem lesz egyensúly, annak ellenére, hogy a tömeg, a sebesség és a lineáris impulzus megegyezik; ugyanez történne, ha $ 6N $ erőt alkalmaznának a $ r $ = $ 2m $ és a $ 6N $ másik ellentétes erejét alkalmazzák a $ r $ = 1 millió USD . Ne feledje, hogy B-nek az F-hez képest még azelőtt volt szögmomentuma, hogy még a pályája mentén elkezdett forogni körülötte, és mindig (p * r) = 12 USD Kg * m ^ 2 / s $ .

2) - Az L meghatározása

A sebességgel (és lineáris lendülettel) rendelkező B test van egy potenciális L forgási momentuma bármely O pontra / testre / körül, amely nem fekszik a pályáján.

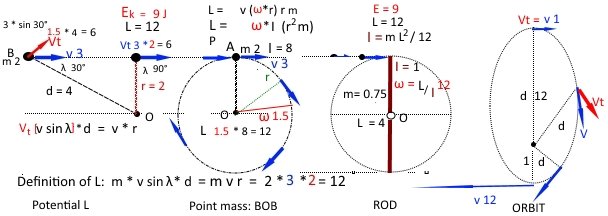
A nagyságrend L-értékét meg lehet szorozni lineáris impulzusával (p = m * v) az O pont távolságával a pályától: $ r $ . A teljes képletben: $ L = m * [v * sinλ * d] $ , L-t megkapjuk, szorozva a tömeget tangenciális sebesség $ V_t = v * sinλ $ szorzat a távolság $ d $ , de $ d * sinλ $ mindig egyenlő a következővel: $ r $

3) - A szögimpulzus megőrzése

szögmomentum L konzerválódik, ha a rendszerre nem vonatkozik külső nyomaték, és ez a tulajdonság segít megérteni a sugár fontosságát. Amikor a B testet O-val köti egy vonal / rúd vagy egy érintés nélküli erő (például g), akkor elkezd körülötte forogni, és tényleges forgási lendületet L kap.

Ha , miközben O körül forog, B hasonló A golyóval hat ( $ m $ = 2, $ v $ span > = 0), B megáll holtan és A ugyanazon v / p / E értéket és L potenciált kapja meg az F pontra hivatkozva, ha ütközik az A inga bobjával ( $ m $ = 2, $ r $ = 2) ugyanazt a v / p / L / E értéket fogja megszerezni. Ha az inga vonala / rúdja $ r_p = k $ , p konzerválódik, de $ L_p $ span > $ L \ times \ frac {k} {r} $ lesz.

Ez egy egyszerű példa, amikor a testet a kerületen forgó ponttömegnek tekintjük, ha a tömeg eloszlik a sugár mentén, akkor egy másik képletet kell alkalmaznunk $ L = I * \ omega $ , ahol $ ω = v / r $ és $ I = m * r ^ 2 $ . P nem konzervált, de KE és L igen, így tudjuk kidolgozni az ütközés kimenetelét. Az L megőrzésének egyszerű példáját itt

találja

Végül a szögmomentum különlegessége ez:

• Nézz fel az égre. Bizonyos fizikai törvények tartoznak ebbe az irányba.
• Nézzen észak felé. Bizonyos fizikai törvények állnak ebben az irányban.
• Nézzen nyugatra. Bizonyos fizikai törvények tartoznak ebbe az irányba.

Azok a fizikai törvények: minden irányban azonosak. Van egy mögöttes konzervált mennyiség, amikor ilyen szimmetriát talál. Hasonló koncepció érvényes, ha kirándul Kínába, a Proxima Centauri-ba, az Andromeda galaxisba, vagy még tovább. Itt a fizika törvényei fordítástól függetlenül megegyeznek. Mi van az idővel? Pislogj a szemeddel, és a fizika törvényei nem változnak. 80 éves kor és a fizika törvényei nem változnak. A fizika törvényei időtlenek.

A fizika törvényeinek időtlensége azt jelenti, hogy az energia konzervált mennyiség. A fizika törvényeinek fordítási függetlensége azt jelenti, hogy a lineáris impulzus konzervált mennyiség. Végül a fizika törvényeinek forgási függetlensége azt jelenti, hogy a szögimpulzus konzervált mennyiség. Ezek mind Noether tételének következményei. Számos más konzervált mennyiség létezik Noether tételéből, és ez nagyon fontosnak bizonyult a kvantummechanika szempontjából. Ez nyilvánvalóan kritikus a klasszikus mechanika szempontjából is. Noether tétele pontosan megmagyarázza, miért konzerválják ezeket a konzervált mennyiségeket.

A szögimpulzus meglehetősen haszontalan fogalom lenne, ha a szögimpulzus nem lenne konzervált mennyiség külső nyomatékok hiányában. Konzervált mennyiség a tér forgásszimmetriájának köszönhetően.

Miért függ a szögimpulzus a pozíciótól?

A szögimpulzus mindig meg van határozva egy referenciaponthoz képest, mondjuk $ \ mathbf r_0 $ span >, (ami gyakran, de nem feltétlenül az eredete).

Ha a rendszer a referenciapont körüli forgás alatt invariáns, akkor azt a mennyiséget, amelyet "szögimpulzusnak nevezünk a $ \ mathbf r_0 $ " tároló konzervált. (Ne feledje, hogy ha csak egy bizonyos tengely körüli elfordulás hagyja a rendszert változatlanul, akkor a szögimpulzusnak csak ez az összetevője konzerválódik.) meglepetés, hogy a szögimpulzus kifejezetten a pozíciótól függ.

Hogyan működik a szögimpulzus megőrzése?

Az absztrakt válasz az Ön rendszerének Noether-tételével és Lagrangianjával foglalkozik. ránéz. Az egyszerűség kedvéért nézzünk csak egy egyenes vonalban mozgó egyetlen részecskét.

Ne feledje, hogy még egy egyenesen mozgó szabad részecskének is bizonyos nulla referenciapontokhoz viszonyított nullszöge van. . Valójában a szögimpulzus csak nulla, ha a lendület és a viszonyítási pont közötti kapcsolat párhuzamos (azaz a referenciapont a részecske útján van).

Noether tétel egy szabad részecskéhez forgatás alatt

Használjuk ezt az ingyenes részecskét, hogy lássuk, honnan származik a $ \ mathbf x \ times \ mathbf p $ ilyen megőrzése. A Lagrangian itt csak a kinetikus energia. Ha elforgatjuk a koordinátákat az origó körül és a rögzített tengely mentén $ \ mathbf n $ a $ \ varphi $ . A kinetikus energiának (a Lagrang-féle) nem függhet a forgásszög től.

A forgatott pozíciókat adja meg a $ \ mathbf x '$ . A kinetikus energia $ \ frac 12 m \ dot {\ mathbf x '} ^ 2 (\ varphi) $ , tehát feltételünk, hogy a kinetikus energia független $ \ varphi $ a következőképpen írható:

$$ \ frac {\ mathrm d (m \ pont {\ mathbf x '} ^ 2 (\ varphi))} {\ mathrm d \ varphi} = \ mathbf p \ frac {\ mathrm d \ dot {\ mathbf x'} (\ varphi)} {\ mathrm d \ varphi} = 0 \ ,, $$

mivel a szabad részecskére nincsenek erők ( $ \ dot {\ mathbf p} = 0 $ ), ezt így írhatjuk: $$ \ frac {\ mathrm d} {\ mathrm dt} \ left (\ mathbf p \ frac {\ mathrm d {\ mathbf x '} (\ varphi)} {\ mathrm d \ varphi} \ right) = 0 \,. $$

Hogyan működik a $ \ mathbf x '$ változik a szöggel? Vessen egy pillantást a végtelen kicsi elforgatásokra vonatkozó fejezetre, és valami olyasmit kell találnia, hogy $$ \ mathbf x '= \ mathbf x + \ varphi (\ mathbf n \ times \ mathbf x) $$

A derivált kiszámítása és a fenti egyenletbe történő bedugása a következőket eredményezi:

$$ \ frac {d} {dt } \ left (\ mathbf p \ frac {d ({\ mathbf x + \ varphi (\ mathbf n \ times \ mathbf x)})} {d \ mathbf \ varphi} \ right) = \ frac {d} {dt } \ mathbf p \ cdot (\ mathbf n \ times \ mathbf x) = \ frac {d} {dt} \ mathbf n \ cdot (\ mathbf x \ times \ mathbf p) = 0 $$

Ami azt mondja, hogy a $ \ mathbf n $ -komponens a $ \ mathbf x \ times \ A mathbf p $ idővel nem változik (azaz konzervált). Ebben az esetben ez a tetszőleges tengelyekre igaz, ami azt jelenti, hogy a $ \ mathbf L = \ mathbf x \ times \ mathbf p $ szögmomentum megmaradt.

Fontoljon meg valami ajtót. Egy darab fa, egyik szélén pánttal. Talán egy méter magas és három méter hosszú.

Most mondd, hogy megpróbálod a helyén tartani az ajtót, a pánttól fél méterre, míg valaki más baseballt dob ​​a az ajtó másik oldala.

Ha a baseball eltalálja a csuklópántot, akkor egyáltalán nem kell nyomkodnia.

Ha a baseball pont ott ütközik, ahol éppen nyomja az ajtót, akkor nagyon sokat kell nyomnia.

Ha a baseball közvetlenül az ajtó három méteres jelére csapódik a zsanértól, akkor sokkal erősebben kell nyomnia. (gondolja, hogy az ujját becsípje egy ajtón)

Annak ellenére, hogy a baseball lendülete mindhárom esetben azonos volt, az első esetben (ha $ r = 0 $ megfelel a zsanérnak) nem A $ \ cdot $ time nyomatékot nem kell alkalmaznia. A másodikban egy kis nyomatékot kellett alkalmaznia, $ \ cdot $ time. A harmadikban nagy nyomatékot kellett alkalmaznia, $ \ cdot $ time.

Ez matematikailag úgy is megfogalmazható, hogy a rendszer szöget zárja le. Természetesen a dolgok kevésbé lesznek intuitívak, ha nem a csuklópántot választja az eredetének, ezért dolgoznia és matekoznia kell annak bizonyítására, hogy a fizikai eredmények megegyeznek. Valójában ez ugyanolyan intuitív, mint a lineáris impulzus, amely függ a referenciakerettől (a rendszert egy másik sebességű keretben tekintve), és véleményem szerint mérföldekkel intuitívabb, mint az energia, amely a referenciakeretétől függ!

A részecske mozgásának leírása többféleképpen lehetséges. Például 2 dimenzióban használhatja a derékszögű $ x, y $ koordinátákat vagy a poláris $ r, \ varphi $ koordinátákat.

Minden koordinátához társíthatunk 'mozgásmennyiséget' vagy ' általános lendület '. Ha egy adott koordináta megfelel a rendszer szimmetriájának, akkor a megfelelő mennyiséget Noether tétele konzerválja.

Mivel a fizika ugyanúgy működik „itt”, mint „át” ott '(azaz megváltoztatja a $ x $ vagy $ y $ értéket), a lineáris impulzus megmarad. Mivel a fizika is ugyanúgy működik, függetlenül a rendszer irányától (azaz a $ \ varphi $ megváltoztatása), a szögimpulzus is konzervált mennyiség.

A radiális komponens azonban nem felel meg a szimmetriának (a $ r $ koordináták megváltoztatása torzulást eredményez), így a sugárirányú impulzus általában nem konzerválódik.

Most térjünk vissza a kérdésre:

Miért a szögmomentum a pozíció függvénye?

Intuitív módon a pozíció hozzájárul a szögimpulzushoz, mert a szögkoordináta megváltoztatása egészen más eredményt eredményez „mozgásmennyiségek” az origótól sugárirányú távolságtól függően.

Ez egy elvont válasz, de rendkívül hasznosnak találom azt a fajta "alapvető természetű" kérdést, amelyhez látszólag tapogatózni szokott. Gondolj két dologra: Noether tétele és egy gondolatkísérlet: "Mi lenne, ha nem látott, de okos lényekként fejlődtünk volna?".

Mint David Hammen Válaszában, Noether tétele, amely azt mondaná nekünk, hogy ha fizikai törvényeink változatlanok a koordinátatengelyeink forgása tekintetében, akkor mégis három konzervált mennyiség létezésére következtetnénk. Technikailag, ha a törvényeit úgy írja le, hogy a legkevesebb cselekvés útját definiálja a Lagrang-féle minimalizálásával, Noether tétele azt mondja Önnek, hogy mindig van egy konzervált mennyiség a Largrangian minden "folyamatos szimmetriájához" - ie minden olyan átalakítás, amely kisebb, azonos típusú transzformációkból valósítható meg, mint a valós számok (gondoljunk csak a szögek összeadására: két tengely körüli elfordulás egy forgáshoz, és összegezzük a szögeket), és így is elhagyjuk a Lagrangian-t változatlan. Törvényeink valóban függetlenek a koordinátatengelyek forgásától, mert az utóbbiak csupán a fizika leírásának részei, nem pedig maga a fizika. Ezek kopernikuszi fogalmak, és Noether tétele valóban megadja azt a képletet, amelyet az AM-re állítasz.

Ahogy David rámutat, az AM-t a természetvédelem teszi hasznossá, nem pedig az, hogy valami forogjon. Ezt érdemes szem előtt tartani, amikor áttérünk a kvantumrészecskék, például az elektronok spinjének tanulmányozására. Hajlamosak vagyunk túlterheltek lenni, ha megpróbáljuk elképzelni ezeket a dolgokat forogni, sőt, Wolfgang Pauli kezdetben egyenesen elutasította az elektronpörgés gondolatát, mert egy kis gömböt úgy kellett forogni, hogy annak határa messze meghaladja a fénysebességet, hogy megmagyarázza a az elektronok. A "valami pörög" fogalma, ahogy azt intuitív módon elképzeljük, nem akadályozná látatlan lényeinket, akik ennek ellenére Noether tételén keresztül következtetnének az AM létezésére: a "pörgés" egy sajátos vizuális tapasztalat, amely történetesen hasznos abban, hogy észleljen valami ellen irányuló mozgást. környezete. Tehát evolúciónk révén ez egy erős vizuális élmény - döntő fontosságú mind a ragadozó, mind a zsákmánylátó állatok életben maradásában, és mindketten vagyunk. Hasznos evolúciós elődeink túlélésére, de nem túl hasznos az alapvető modern fizika számára: még a nagy Wolfgang Paulit is megbuktatta.

Nézze meg a videót itt

Remélem, hogy amikor látja, hogy az ember forog és mozgatja a súlyokat (megváltoztatva a $ r $ értéket), láthatja, hogy $ r A $ fontos.

Ne feledje, hogy az $ r $ egy távolság a forgó objektum egyes részeitől a forgástengelyig (ami nem teljesen azonos a pozícióval)

A szögimpulzus a p = mv lineáris impulzus analóg fogalma, amelyben m a test tömege és v annak sebessége.

Most nézze meg, honnan jön a szögmomentum. Vegyük figyelembe az egyszerűség kedvéért egy testet, amely egy tengely körül egy körön mozog, és legyen ω a szögsebesség, vagyis az a szög, amellyel a tárgy forog, egységnyi idő alatt. A lineáris és a szögsebesség kapcsolata

$$ v = \ omega r. \ tag {1} $$

Az objektum mozgásának energiája $ E = (1/2) mv ^ 2 $, és az (1),

$$ használatával E = \ frac {1} {2} mr ^ 2 \ omega ^ 2. \ Tag {2} $$

Ezután kényelmes meghatározni a tehetetlenségi lendület nevű mennyiséget, $ I $

$$ I = mr ^ 2, \ tag {3} $$

és kapjon egy képletet, amelyben szögletes, nem lineáris sebességet használunk

$$ E = \ frac {1} {2} I \ omega ^ 2. \ Tag {4} $$

A tehetetlenségi lendület fogalmát folytatva szögletes lendületet kapunk , $ L $

$$ L = I \ omega, \ tag {5} $$

hasonló a lineáris momentumhoz $ p = mv $, azaz mint $ \ omega $ a $ v $, $ I $ helyettesíti a $ m $ értéket. Ebben a képletben $ I $ helyettesítése a (3) kifejezésből

$$ L = mr ^ 2 \ omega = mvr. \ tag {6} $ $

Ez a válasz arra a kérdésére, hogy miért szorozzuk meg $ r $ -val. De, amit fentebb mondtam, akkor érvényes, ha a mozgás kör alakú. Általánosabb mozgáshoz

$$ \ vec {L} = m \ vec {v} \ times \ vec {r}, \ tag {7} $$

ahol A $ \ vec {L} $, $ \ vec {v} $ és $ \ vec {r} $ vektorok, a $ \ szor $ pedig a vektor-szorzót jelöli.

Sok szerencsét

Talán így láthatja:

A vektor szorzás modulusa a következő:

$$ | \ mathbf {L} | = | \ mathbf {r } \ times \ mathbf {p} | = rp \ sin {\ hat {rp}} $$

ahol láthatja a szögimpulzus fő jellemzőjét: a szükséges helyzetnek a helyzetét és lineáris momentumát egyszerre legyenek arányosak a $ L $ -val és fordítottan kapcsolódjanak egymáshoz.

Így garantálja az olyan jelenségek leírását, mint a táncoló korcsolyázó forgatása: amikor a karokat a testhez húzzuk, a forgás megnő, megőrzi a $ \ mathbf {L} $ értéket.